Calculando con cacumen y un refresco para enfriar las neuronas

No se deje impresionar por estas operaciones aritméticas, y utilice los datos que les doy para que lleguen a la respuesta correcta. Y si sube mucho la temperatura neuronal, vaya de inmediato para el refresco.
I
En las siguientes ecuaciones todos los números son naturales mayores que 1, y ninguno pasa de 2 dígitos, es decir todos son menores que 100.
Despeje todas las incógnitas
Si lo demuestra es mucho mejor.
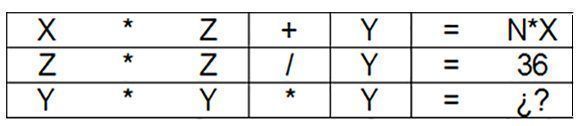
II
El colmo de un abogado es ______________________________________________.
Si no llega a tres posibles respuestas, debe ponerle más empeño a los acertijos que cada semana les planteo.
Recuerden que:
“Es preferible una solución insignificante salida de cabeza propia; que una genial copiada de otro, sobre todo sin entenderla”. NGPA
- Ideas creativas para un mejor impacto de las telenovelas en el desarrollo de nuestra sociedad
- Respuesta a “Psicología, matemática y Girón de la Victoria, a seis m”
- Psicología, matemática y Girón de la victoria, a seis m
- Respuesta a “Ecos de un encuentro inolvidable inspirado por la matemática y la creatividad”
- Ecos de un encuentro inolvidable inspirado por la matemática y la creatividad
- ir aPara Pensar... »
- Palante en Cubadebate: Nadie nos quitará el mes de abril (+ PDF)
- Ideas creativas para un mejor impacto de las telenovelas en el desarrollo de nuestra sociedad
- 🎧 Modo Avión: Cuando un amor termina (+ Podcast)
- Playa Gallina: Ambiente tranquilo, natural y sano
- S05E14: Análisis del primer videojuego cubano que llega a consolas de nueva generación
- ir aEntretenimiento »


Si a Z le damos el valor de 12, entonces Y va a ser igual a 4, en la ecuación número II.
Luego la ecuación III va a dar como resultado 64.
Si a X le damnos valor 2, luego N, despues de resuelta la ecuación I, tomará el valor de 14.
No se me dan bien las mates así que respondo el 2do: El colmo de un abogado es perder el JUICIO, o tener un hijo jorobado que estudie Derecho.
R. Z = 12
Y= 4
N=14
X=2
1) X*Z+Y=NX
2*12+4=14*2
24+4=28
28 = 28
2)Z*Z/Y=36
12*12/4=36
144/4=36
36=36
3)Y*Y*Y=?
4*4*4=64
Gracias Nestor
Y=4, Z=12, X=1(2), N=16(14).
Muy interesante acertijo y broma del ilustre Prof. Nestor del Prado Arza
Y= 4, Z=12, X=2, N=14
Las ecuaciones serian:
Primera ecuación, (2 x 12) + 4 = 14 x 2
Segunda ecuación, (12 x 12) / 4 = 36
Tercera ecuación, 4 x 4 x 4 = 64
El colmo de un abogado es:
Decirle a un mudo que tiene derecho a guardar silencio
Acusar cansancio tras un largo juicio
Que nunca le salga la muela del juicio
Despejo la segunda ecuación
Z*Z = 36 * Y
Qué número al cuadrado da como resultado un múltiplo de 36:
Z = 6 , Y = 1
Z = 12 , Y= 4
Z = 24, Y= 16
(...)
Como tienen que ser mayor que 1, tomo la segunda Z = 12 , Y= 4
Luego: Y * Y * Y = ¿? -> 4 * 4 * 4 = 64
Para la primera: X * Z + Y = N * X
se puede transformar en
Z * X – N * X = - Y
(Z – N) * X = - Y
(12 - N) * X = -4
N = 13 , X = 4 Ó N = 14 , X = 2
N = 16 , X = 1 No puede ser porque tienen que ser mayor que 1.
De las posibles respuestas doy como solución: N = 14 , X = 2 , Z = 12 , Y= 4 y ¿? = 64
N=16, X=1, Z=12, Y=4, ?=64...
Respuesta al ejercicio I
Este Ejercicio puede tener muchisimas respuestas(8 en total)! Les explico 2
z * z / y = 36 Es la clave de todo al ser todos números naturales eso implica que Z es divisible por Y y partiendo de ahí hay que encontrar un cuadrado que sea divisible por 36.
144 y 324 lo son primeros.... probemos 12 * 12/ y = 36 ... y = 144/36 = 4 luego 12x+4= Nx
4 = Nx -12x .... ummm esto no pinta nada pero que más da ...aqui no queda más que evaluar X para hallar N ... x= 2?? ... 4 = 2N -24 ... 28 = 2N N=14 ... Y final Y*Y*Y = 4 * 4 *4 = 64
324 .... 18 * 18 / y = 36 ... 324/36 = y .... y = 9 .... de nuevo 18x + 9 = Nx ... 9 = Nx - 18x .. probemos x= 3 .... 9 = 3N - 54 ... 54-9 = 3N ... 45 = 3N ... N = 45/3 = 15 ... Y*Y*Y = 9*9*9 = 729
Ding ding ... campanita ¿Z es mulitplo de 6? ¿"Y" siempre tendrá raíz cuadrada? Si y si .. la primera ecuación es irrelevante(Al menos para mi)!
Z = 12, 18, 24, 30, 36, 42, 48 , 54
Y = 4, 9,16, 25, 36, 47, 64, 81
Y*Y*Y = 64, 729 , 4 090, 15 625, 46 656, 103 823, 262 144, 531 441
Bien como los números son naturales eso implica que son enteros y positivos. Además mayores que 1 y menores que 100.
Lo primero que hice fue trabajar la primera ecuación:
Y*Y*Y=¿?
Y³=¿?
Busqué las Y que dieran números entre 1 y 100 al ser elevadas al cubo, estas fueron 1, 2, 3 y 4, descartando el 1 porque ya se dijo que los números serían mayores que 1 (no mayores e iguales).
Al sustituir Y =2; 3 y 4 en la segunda ecuación:
Z*Z/Y=36
Z²=36*Y, se descartó Y=2 y Y=3 porque 36*2=72; Z=8.48 y 36*3=108; Z=10,39;
quedando Y =4 y Z=12 ; Z=(36*Y)^1/2=(36*4)^1/2.
Con Y=4 y Z=12 se sustituyó en la primera ecuación X*Z+Y=N*X y quedó:
X*12+4=N*X
X*12- N*X=-4
X(12-N)=-4
Los pares de números enteros que multiplicados dan -4 son -2 y 2 y -4 y 1, -2 y -4 serían los resultados de (12-N) quedando X=2 y X=1por la razón de ser números mayores que 1 se descarta la pareja (12-N)-4 X=1 quedando X=2 y (12-N)=-2; N=14.
Entonces X=2; Y=4; Z=12; N=14
X*12+4=N*X
2*12+4=14*2
24+4=28
28=28
Z*Z/Y=36
12*12/4=36
144/4=36
Y*Y*Y=¿?
4*4*4*=64
Me fui por el refresco y busqué a un abogado, y me dijo:
Es perder la muela del juicio, y de paso me hizo este chiste: Un avión lleno de abogados fue secuestrado y la amenaza que se escuchó fue: - ¡Cumplan con nuestras exigencias o liberaremos a dos cada hora!
Que bueno este amigo me hace recordar algo de las Matématicas.Respt.-N=14,X=2,Y=4,Z=12.Todos múltiplos del 2 ,naturales y menores de 100.
2-z*z/y=36=z*z=36*y=12*12=144=36*4=144=144(Pruebas deductivas)
3-y*y*y=?=4*4=16*4=64
1-(x*z0+y=n*x-(2*12)+4=28=N*X=28=28/2*N=28/2=N=14
.En cuanto al II El colmo de un Abogado es No tener nada que defender.Gracias y esperamos la próxima aventura.
Nestor me costó trabajo resolverlo, muy bueno.
1ero como dices hay que tener muy en cuenta los datos que das, el tema que todos son números naturales y 2do que son valores menores que 100. O sea, del 1 al 100. El 0 no es un número natural.
De aquí entonces despejé las variables:
Z=6√Y
Y= Z2/36
N= (X * Z + Y)/X
X= (X * Z + Y)/N
Y3 = ¿?
De la primera ecuación los resultados posibles teniendo en cuenta que, Y es un número natural del 1 al 100 y que Z también, la raíz de Y debe ser un número natural también de ahí que tengamos los siguientes resultados posibles para Y y Z: 1 y 6; 4 y 12; 9 y 18; 16 y 24; … ; 81 y 54.
Si sustituimos estos resultados en la ecuación 3 o 4 entonces el único que daría a X o N como número natural de 1 a 100 sería para Y=9, Z=18, X=3 y N=21.
Comprobando los resultados tenemos que:
Z=6 √9 =6*3=18
N= (X * Z + Y)/X
21= (3*18+9)/3
21= (54+9)/3
21= 63/3
21=21
93= ¿?
891= ¿?
Saludos
Dsiculpa es que la respuesta salieron mal las potencias
bueno cuando vean algo raro como que 93 = 891 es un problema de escritura en realidad lo que quería decir era que 9 a la 3 es 729
N=7
x=1
y=1
z=6
Empezamos trabajando con la ecuación z^2 / y = 36=6^2, de donde obtenemos y = (z/6)^2 o sea que y es un cuadrado perfecto >2 y <99, que pueden ser 4, 9,16,25,36,49,64,81 … o valores.
Los pares (z,y) serian:
(12,4) (18,9) (24,16) (30,25) (36,36) (42,49) (48,64) (45,81)
A cada uno de estos pares (z,y) se les calcula la x como cualquier divisor de y, dado que y = x(N-z) , distinto de 1.
Y luego N = y/x + z
Al final lo que tiene los ¿? que imagino que sea lo que se quiere son los valores de Y^3 podrían ser los valores.
4^3, 9^3, 25^3, 36^3, 49^3, 64^3, 81^3
Saludos
y por que ¿? tiene que ser menos que 100, si eso no es ningun numero ???? ... entendi que los que tenian que ser menos que 100 eran x,y,z,N
¿Puedes asegurar que esos signos de interrogación no representan a un número?
De cualquier manera interpretarlo como usted hizo sería otro acertijo de mayor complejidad. Ya lo comentaré en mi respuesta del próximo lunes16. Gracias por involucrarse en serio en Para Pensar...
Respondiendo a un comentario que leí......Si lo signos de interrogación fueran un número mayor que 100, no se cumpliera que Y está entre 1 y 100.
Acá envío mi respuesta, delante de mi una hojita llena de cálculos, envío algún datico de mi razonamiento.... Yo comenzé buscado Y en la tercera ecuación, un número menor que 5 porque 5 al cubo daba un número mayor que 100, y mayor que 1.
Le asigné a Y = 4 y lo sustituí en la segunda, obtuve Z = 12.
Realizé algunos despejes en la primera ecuación y sustituciones obtuve X = 1, como tiene que ser mayor que 1, probé con X = 2, sustituí y despejé N, N = 14.
Los resultados finales Y = 4, Z = 12, X = 2, N = 14. Estos valores cumplen con las restricciones.
II. El colmo de un abogado es perder el Juicio............y terminar en Vivienda.
Estimados acertijandos, no es igual comprobar que fundamentar el razonamiento. Tal vez al decir demostrar entendieron que no se debía evidenciar el método empleado aunque fuese el socorrido tanteo inteligente. Espero que algún matemático saque la cara evidenciando una demostración elegante.
Estimado profesor Néstor del Prado Arza. También deseo que un matemático saque la cara y coincido con usted que comprobación y fundamentar el razonamiento son cosas bien diferentes.
El colmo de un matemático. "Sembrar una mata de papaya y que le salga la raíz cuadrada", o tener cálculos en la vesícula" o incluso "que nunca haga ejercicios"
Por razones de estricta confidencialidad me reservo los colmos de un ingeniero.
Gracias amigo Oro, ya tendré en cuenta al ingeniero para un próximo ejercicio de los colmos. Jajajaja. Ah y también el del matemático.
Intente hacerlo por despeje pero me fue muy difícil por las cantidades de incógnitas y tuve que recurrir al tanteo por lo que envió dos respuesta
2 12 4 28
12 12 4 36
4 4 4 64
x=2
z=12
y=4
N=14
4 12 4 52
12 12 4 36
4 4 4 64
x=4
z=12
y=4
n=13
I- X=1; Y=1; Z=6 y N=7 No me dicen que a las variables no se le pueden asignar el mismo número.
II- El colmo de un abogado es declararse culpable de un crimen que no cometio
Ya veo que algunos acertijandos se han complicado al no interpretar bien el enunciado. Yo dije que todos los números de las ecuaciones, no todas las variables no pasaban de 100. Como sé que Alfredo Galano y Darwinazo saben bastante Matemática, les sugiero revisar sus respuestas
Rectifico, no pasaban de 99. Es lo matemáticamente correcto.
Mi solución:
(1) xz+y=nx
(2) zz/y= 36
(3) yyy=??
De (2):
y=zz/6*6
Como “y”es un número natural mayor que 1, entonces z>6 y con valores múltiplos de 6:
12 (y=4), 18 (y=9), 24 (y=16), 30 (y=25), 36 (y=36), 42 (y=49), 48 (y=64) y 54 (y=81), porque para z=60 (y=100), pero y0 para que se obtenga un número positivo (y), pues x es un número natural.
Luego:
n>z, pues z y n también son números naturales.
Así, n>12
De (5):
x= y/(n-z)
Probando los primeros valores y=4, z=12 tendríamos que tomar un valor de “n”mayor de 12, digamos, 13.
x=4/(13-12)=4
Y esos valores cumpen la ecuación (1) xz+y=nx
4*12+4=13*4=52
Probando n=14:
x=4/(14-12)=2
Y esos valores también cumpen la ecuación (1) xz+y=nx
2*12+4=14*2=28
Probando n=16:
x=4/(16-12)=1
Pero x>1, de modo que n no puede ser 16, ni valor mayor que 16.
Así que, RESPUESTAS:
x=2,4
y=4
z=12
n=13,14
y3=64
Bien profesor... deje ver como razono esto:
la cuestión esta en la segnda ecuación... tenemos que Z^2 = 36 y
Como ambos términos son cuadrados perfectos en principio Y es un cuadrado perfecto..
como Z es menor que 100, entonces 36 y debe ser menor a 9081 (que es el cuadrado de 99) con lo cual Y tiene un valor entre 1 y 16
Tenemos igualmente que Y = Z^2/36 o o que es lo mismo Y = (z/6)^2, como estamos en el mundo de los números naturales, significa que la sqr (Y) es un numero natural, menor que 16
queda entonces: sqr(Y) = Z/6
Y es un número natural menor que 16, cuadrado perfecto y multiplo de 6... Los multiplos de 6 cuadrados perfectos y menores a 16 son: 6 y 36 y como z/6 es un numero natural, el valor de Z=6
por lo cual el valor de Y, es 1
Sustituyendo en la 1ra ecuación quedaría
X*6+1 = N*X
o sea
6X+1 = NX
NX-6X=1
factor comun x
X(N-6) = 1
como son sumeros naturales
x= 1
N-6 =1
N=7
resolviendo
1*6 + 1 = 7*1
6*6/1 =36
1*1*1= 1
El como de un abogado es perder la muela del juicio
(1) X*Z+Y=N*X
(2) Z*Z/Y=36
(3) Y*Y*Y=¿?
De (3):
Y*Y*Y<100
Y^3<100
Y< Raíz cúbica de 100
Y< 4.64
1<Y<=4 es el intervalo de validez de Y
De (2):
Z^Z=36*Y
Z= Raíz cuadrada de (36*Y)
Tanto Y como Z tiene que ser números naturales. Eso se cumple solo para Y=4
Se obtiene entonces:
Z= Raízcuadrada(36*4)
Z=12
De (1):
X*Z+Y<100
X*12+4<100
12*X<96
X<96/12
X<8
1<X<8 es el intervalo de validez de X
De (1):
N=(X*Z+Y)/X
Pero N también tiene que ser natural mayor que 1.
Eso se cumple sólo para X=2
N=(2*12+4)/2
N=14
Resultado:
X=2
Y=4
Z=12
N=14
(1) 2*12+4=14*2
(2) 12*12/4= 144/4 = 36
(3) 4*4*4=64
Colmo de un abogado:
1- Perder el juicio.
2- Ser zurdo y tener que ejercer el Derecho.
3- Ser un caso perdido.
4- Perder las muelas del juicio.
5- Que su cliente que se llame Inocente y sea hallado culpable.
6- Que su mujer se llame Norma y no poder contradecirla.
Saludos...
Amigo Benjamin, los números deben ser mayores que 1, Revaloriza que cacumen matemático te sobra.
-1-
YE sería igual a cuatro,
ZETA doce, EQUIS dos,
ENE da catorce y los
SIGNOS son sesenta y cuatro.
Ya puestos todos los datos
El colmo de un abogado
Es llegar a casa cansado
Y que le toque también
El Banquillo, porque estén
Los sillones ocupados.
-2-
Otro colmo, en realidad,
Sería tener que juzgar
A un piloto por violar
La ley de la gravedad.
Un buen traje y la verdad
Son el sello distinguido
Del que este oficio ha elegido
Y el colmo de un abogado
Es entrar en un juzgado
Solo de “bolas” “vestido”.
Super decimas, que original!
Para la solución de este acertijo lo llevé a mi casa para involucrar a mi hija, que estudia en la Vocacional en el grado 10mo, acá en Holguín. utilizamos el método de tanteo después de despejar variables en la fila 1 y 2 llegando a las siguientes ecuaciones:
fila 1: dividiendo en ambos miembros por X quedaría: Z+ Y/X = N
fila 2: (Z*Z)/Y = 36
Utilizando esas dos ecuaciones podemos encontrar varios juegos de números que la cumplan como por ejemplo:
1.- Y=4, Z=12, X= 2 Y N= 14: El resultado en la fila 3 sería: 64
2.- Y=4, Z=12, X= 4 Y N= 13: El resultado en la fila 3 sería: 64
3.- Y=9, Z=18, X= 9 Y N= 19: El resultado en la fila 3 sería: 729
4.- Y=16, Z=24, X=2 Y N= 32: El resultado en la fila 3 sería: 4096
cuando el profe refiere que todos los números serán mayores que 1 y menores que 100, asumimos que serían las variables y no los productos resultantes de su combinación.
Encontramos una combinación donde X=1, pero mi niña se percató que los números tenían que ser mayores que 1, por tanto no cumplía con la condición.
Para el colmo, mi hija dijo: El colmo de un abogado es defender a quien lo agrede.
Yo afirmo con un toque de gracia: El colmo de un abogado es: Tener que defender en un juicio a la suegra y perder tres veces: El Juicio, la Suegra y a la Esposa....
Rene, me emocionó mucho esta colaboración padre-hija. Si no tienes inconveniente dime el nombre de tu niña. Me hace muy feliz que una estudiante de tan prestigiosa Vocacional; ahora IPVCE me siga. Excelentes los colmos.
Profe, gracias por su detalle, mi hija se llama: Yaimé Riverón Paneca y créame, es la mejor hija.... Gracias
Hola pues aquí va mi respuesta y como la obtuve:
I) X*Z + Y = N*X
II) Z**2 / Y = 36
II) Y**3 = ¿?
despejando en II se obtiene:
IV) Z**2 = 36*Y
Hice una pequeña trampa para saber cuantas combinaciones de Z y Y cumplen esta condición para valores entre 1 y 100, En un terminal de Python, ejecute el código:
for z in range(1, 100):
for y in range(1, 100):
if z**2 == 36*y:
print('y = {} ; z = {} '.format(y, z))
la salida de esto da:
y = 1 ; z = 6 # esta está descartada porque no cumple con la restricción > 1
y = 4 ; z = 12
y = 9 ; z = 18
y = 16 ; z = 24
y = 25 ; z = 30
y = 36 ; z = 36
y = 49 ; z = 42
y = 64 ; z = 48
y = 81 ; z = 54
después de esto es evidente que el problema tiene múltiples soluciones. con estos resultados podemos acotar I hasta encontrar las respuestas correctas y ampliando el script de python a:
rslt = []
for z in range(1, 100):
for y in range(1, 100):
# evaluando en IV
if z**2 == 36*y:
if y == 1 or z == 1:
# eliminando los valores que sean 1
continue
rslt.append([y, z])
for yz in rslt:
print('y = {} ; z = {} '.format(yz[0], yz[1]))
for x in range(1, 100):
for n in range(1, 100):
# evaluando I
if (x*yz[1] + yz[0]) == (n*x):
if x == 1 or n == 1:
# eliminando los valores que sean 1
continue
print(' x = {}; n = {}; y**3 = {}'.format(x, n, yz[0]**3))
obtenemos todas las posibles combinaciones y resultados de Y**3. este script le toma a mi ordenador 0.0054 ms en resolverse. Saludos y gracias por el reto
y = 4 ; z = 12
x = 2; n = 14; y**3 = 64
x = 4; n = 13; y**3 = 64
y = 9 ; z = 18
x = 3; n = 21; y**3 = 729
x = 9; n = 19; y**3 = 729
y = 16 ; z = 24
x = 2; n = 32; y**3 = 4096
x = 4; n = 28; y**3 = 4096
x = 8; n = 26; y**3 = 4096
x = 16; n = 25; y**3 = 4096
y = 25 ; z = 30
x = 5; n = 35; y**3 = 15625
x = 25; n = 31; y**3 = 15625
y = 36 ; z = 36
x = 2; n = 54; y**3 = 46656
x = 3; n = 48; y**3 = 46656
x = 4; n = 45; y**3 = 46656
x = 6; n = 42; y**3 = 46656
x = 9; n = 40; y**3 = 46656
x = 12; n = 39; y**3 = 46656
x = 18; n = 38; y**3 = 46656
x = 36; n = 37; y**3 = 46656
y = 49 ; z = 42
x = 7; n = 49; y**3 = 117649
x = 49; n = 43; y**3 = 117649
y = 64 ; z = 48
x = 2; n = 80; y**3 = 262144
x = 4; n = 64; y**3 = 262144
x = 8; n = 56; y**3 = 262144
x = 16; n = 52; y**3 = 262144
x = 32; n = 50; y**3 = 262144
x = 64; n = 49; y**3 = 262144
y = 81 ; z = 54
x = 3; n = 81; y**3 = 531441
x = 9; n = 63; y**3 = 531441
x = 27; n = 57; y**3 = 531441
x = 81; n = 55; y**3 = 531441
El colmo de un abogado es perder el juicio.
I. De la ecuación de la fila II se tiene que z2(z al cuadrado)=36y. Como todos los números son naturales y menores que 100, el único cuadrado perfecto divisible por 36 es el propio 36 (144, 324,… tienen más de 2 dígitos). De lo cual se obtiene que z =6 y y=1 y la ecuación de la fila III sería: y.y.y=1.
De la ecuación de la fila I se tiene entonces que 6x + 1= Nx y si x(N-6) =1, entonces x=1y N =7.
II. El colmo de un abogado es:
1. Perder su juicio.
2. Estudiar derecho siendo jorobado.
3. Defender a su defendido un Día de la Defensa y perder el juicio.
otro colmo de un abogado: Tomar mucho refresco y no tener cacumen, je,je,je
Amiga Rosa Fipa, los números son mayores que 1. Vuelve a ponerle tu genial cacumen.
Je, je, olvido de una condición = falta de cacumen, pero como bien apunté la fila 2 de la columna 1 sería 144 (z al cuadrado) que es mayor que 99…y ahí estuvo mi trago de refresco. Entonces, si es posible, z =12 y y=4 y para que x(N-12) sea igual a 4, se cumplen solo las condiciones para x = 2 y N=14…¿aprobado?
...y sigo tomando refresco. También se cumple para x=4 y N=13 (Había desechado la posibidad de (N-12)=1)
Si todos los números son números naturales mayores que 1 y menores que 100, entonces.
En la ecuación (3):
Y solo puede tomar los valores 2, 3 y 4 para que cumpla la condición dada, porque 2*2*2=8; 3*3*3=27 y 4*4*4=64 pero de ahí en lo adelante 5*5*5=125; ………. que es mayor que 100 y no cumple con la condición dada.
Si Y=2, en la ecuación 2, Z es la raíz cuadrada de 72 que es ≈ 8.49 que no cumple la condición.
Si Y=3, en la ecuación 2, Z es la raíz cuadrada de 108 que es ≈ 10.39 que tampoco cumple la condición.
Si Y=4, en la ecuación 2, Z es la raíz cuadrada de 144 que es 12 que cumple con la condición dada.
Por lo tanto, tenemos definido que Y=4 y Z=12.
Sustituyendo estos valores en la ecuación 1:
X*12+4=N*X
4=N*X-X*12
4=X(N-12)
X=4/(N-12) Para que X cumpla con la condición, N tiene que ser obligatoriamente igual a 14 por lo que: X=4/(14-12); X=2 (Si N=16 X=1 y no cumple. Para valores de N mayores de 16, X es menor que 1)
Por lo tanto los valores son: X=2, N=14, Z=12, Y=4, ¿?=64
Las respuesta es: x=2
y=4
z=12
N=14
z*z/y=36 z2 /y= 36 z2 =36y
y no puede ser 1 por condición inicial, pero debe ser un número natural menor que 100 que tenga raíz cuadrada.
Probando con y=4
z2 =36*4 z=12
vamos a la primera ecuación:
xz+y=Nx
12x+4=Nx ; 4= x * (N-12) por tanto 4/x = (N-12) lo cual se cumple para x=2 y N= 14
Comprobando el todas las ecuaciones
x*z + y = N*x
2*12 + 4 = 14*2
24 4 =28 =28
z*z / y =36
144 / 4 =36
Por último e importante y3=64 que cumple que es menor que 100
Je, je, olvido de una condición = falta de cacumen, pero como bien apunté la fila 2 de la columna 1 sería 144 (z al cuadrado) que es mayor que 99…y ahí estuvo mi trago de refresco. Entonces, si es posible, z =12 y y=4 y para que x(N-12) sea igual a 4, se cumplen solo las condiciones para x = 2 y N=14…¿aprobado?
Bueno, tomando como punto de partida la eciación
Z2/Y=36
tenemos que la raiz de Y = Z/6
por lo tanto de aqui sacamos que Y debe ser un cuadrado perfecto y Z divisible por 6
tomando los números menores que 100 y mayores que 1, las parejas que cumplen esto son:
(Y; Z)= (1; 6), (4; 12), (9; 18), (16; 24), (25; 30), (36; 36), (49; 42), (64; 48), (81; 54)
Ahora tomemos XZ+Y=XN, despejando N = (XZ+Y)/X
Por lo tanto (XZ+Y) tiene que ser divisible por X y esto nos reduce las posibilidades, entonces tomando las 9 combinacions anteriores de Y y Z y manteniendo que todas las variables están entre 2 y 99, inclusive, tenemos las siguientes soluciones:
(X; Y; Z; N)=
(4; 4; 12; 13)
(2; 4; 12; 14)
(3; 9; 18; 21)
(9; 9; 18; 19)
(2; 16; 24; 32)
(4; 16; 24; 28)
(8; 16; 24; 26)
(16; 16; 24; 25)
(2; 36; 36; 54)
(4; 36; 36; 45)
(2; 64; 48; 80)
(4; 64; 48; 64)
(8; 64; 48; 56)
(16; 64; 48; 52)
De aquí las opciones posibles para Y3 serían 64; 729; 4096; 46656 y 262144.
En el enunciado no dice que los números deben ser diferentes, pero si así fuera, se eliminarían las opciones 1; 4; 8; 9; 10 y 12.
Bueno... después de perder tanto tiempo y escribir tanta... "cacumen", veo la respuesta de Nestor a Alp. diciendo que también se pueden interprestar los signos "¿?" como una variable, aunque matemáticamente sólo estarían representadas como variables X; Y, Z y N, pero tomando en cuenta esa posibilidad, entonces Y3 también debería ser menor que 100, reduciendo mi respuesta anterior a sólo 2 combinaciones:
(X; Y ; Z; N) = (4; 4; 12; 13) y (2; 4; 12; 14) y repitiendo la conjetura que hice en mi respuesta anterior de que cada variable de ser no repetida, nos quedaríamos sólo con la segunda.
Saludos