Solución al problema del dibujo de figuras sin levantar el lápiz
Voy directo al punto para los impacientes y los súper pragmáticos; luego daré las explicaciones para quienes deseen aprender algo nuevo o recordar cosas pasadas.
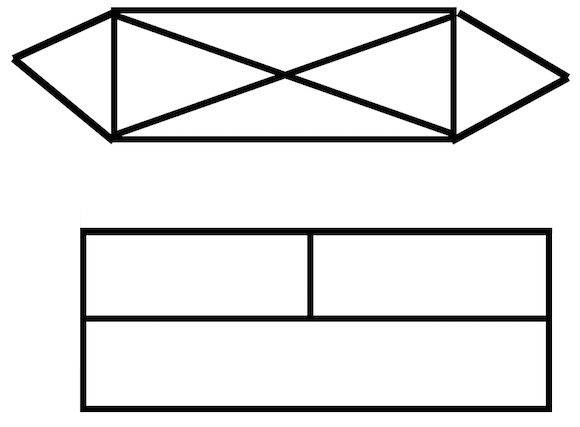
La primera figura se puede dibujar de un solo trazo, es decir sin levantar el lápiz ni repetir segmento alguno.
En la segunda es imposible hacerlo, hay que levantar el lápiz una vez. La base teórica de este tipo de problemas radica en la llamada geometría de posición o topología, en que no importa las dimensiones de las partes que componen la figura sino el orden en que están dispuestas.
El genial matemático Euler, estudio este tipo de problema, en particular se relata la solución del llamado problema de los siete puentes sobre el río de una isla del Kaliningrado de la extinta URSS. El problema consistía en determinar si se podían cruzar los siete puentes sin pasar por alguno más de una vez. Pero no voy a extenderme sobre este bello problema y su solución.
Vamos a centrarnos en el problema publicado en Cubadebate.
En estos tipos de figuras cerradas, existen dos clases de nodos o puntos de intersección de segmentos: los pares que son aquellos en que convergen un número par de segmentos; y los impares en que convergen un número impar.
Hay tres posibles casos de solución del problema. Hay figuras que siempre se pueden dibujar sin importar el punto en que se comience. Otras se pueden dibujar de un solo trazo cuando se comienza desde puntos determinados. En el tercer caso es imposible hacerlo, como en la figura 2 planteada.
Veamos el algoritmo para determinar en qué caso estamos, en dependencia de la cantidad de puntos o nodos pares e impares.
- Si la figura no tiene puntos impares, siempre se podrá dibujar de un solo trazo, comenzando por cualquiera.
- Si la figura tiene solo un par de puntos impares, se podrá dibujar de un solo trazo, comenzando por uno de ellos, y se terminará en el otro.
- Si la figura contiene más de un par de puntos impares, no podrá dibujarse de un solo trazo.
En la figura 1 no hay puntos impares, note que en cada uno salen o llegan una cantidad par de segmentos (dos o cuatro). Por tanto se puede dibujar de un solo trazo.
En la figura 2 hay cuatro puntos impares, por tanto como dijo apg, la respuesta es NTS. Algunos foristas han dado excelentes explicaciones.
Saber que un problema no tiene solución es una especie de solución. Es decir el conjunto solución es nulo o vacío. No ha sido mi intención hacerles perder tiempo ni mucho menos burlarme de ustedes. Insisto en la importancia que tiene la demostración matemática que un problema dado no tiene solución.
El forista Kindo me ha motivado a contar la siguiente anécdota, que al leer otros comentarios veo que también les sucedió algo parecido. En mi etapa de profesor de matemática y computación en la Escuela Vocacional Lenin, allá por los años 70 del pasado siglo, trabajé este tipo de problemas con los alumnos a los que entrenaba para las olimpiadas de matemática. A uno de ellos se le ocurrió divulgar un problema parecido al de la figura 2, y se produjo una verdadera fiebre por intentar resolverlo. Se gestó la leyenda que yo era el único que sabía resolverlo, pero que si alguien lo resolvía se ganaría un automóvil Mercedes Benz, donado por un ilustre empresario de esa firma que había visitado el Centro de Cálculo de la Escuela.
En cuanto al intento de solución creativa de Arturo y de Horus, quienes proponen doblar el papel, es loable pero cambia la esencia del problema. De cualquier manera hay que aprender de los foristas innovadores, así que a partir de ahora añadiré que no se vale doblar el soporte en que se dibuje la figura.
Espero haber complacido a la mayoría de los que se involucraron en este problema.
Para Sergio, Kindo y tal vez otros que participan pero sin hacer comentarios aunque lo disfruten, les aviso que en las próximas publicaciones gozaremos de lo lindo, ejercitando la mente.
Gracias por vuestra participación pública, sin ella todo perdería su encanto.
- Comienza la XXIII Cumbre del ALBA-TCP: Nuevo capítulo en la integración Latinoamericana (+ Video)
- Pedro Sánchez pausa agenda pública para reflexionar sobre su futuro como presidente de España
- Las garras del bloqueo se extienden a Argentina: Cubana de Aviación suspende vuelos por negativa de proveedores
- Ministro de Transporte cubano llega a Irán en visita oficial
- José Ramón Pelier gana el boleto olímpico a París 2024
- ir aNoticias »
- Palante en Cubadebate: Nadie nos quitará el mes de abril (+ PDF)
- Ideas creativas para un mejor impacto de las telenovelas en el desarrollo de nuestra sociedad
- 🎧 Modo Avión: Cuando un amor termina (+ Podcast)
- Playa Gallina: Ambiente tranquilo, natural y sano
- S05E14: Análisis del primer videojuego cubano que llega a consolas de nueva generación
- ir aEntretenimiento »


ja...ja...ja......el primero claro que sin problemas muchos lo hicimos....periodista me tuviste varias horas en eso...buen reportaje, gracias, hoy aprendí algo nuevo.
ah!!! hoy es domingo y como sabe no muchos tenemos el placer de acceder a la web si no estamos en el trabajo o la escuela, por eso no hay comentarios, seguro mañana lloverán.
Correcto
Un saludo desde Puerto Rico...para decirme que soy fanático de sus retos...enhorabuena...y mis saludos a Jose Conception Llanes...
Muchas gracias a Néstor con tantos problemas y desgracias que tenemos hoy en los dias y no estamos ajenos a ello, se le agradece un artículo así que te saca por un instante de la realidad y me lleva hasta mis años de Universidad
Biennn, claro que NTS...lo sierto es que nos tuvo muchos dias en pensando..jajajaja
Me recuerdo del Mercedes en premio por resolver aquel problema..... muchos decían que doblando el papel se resolvía.. Pero ahora mismo la mente me falla, no recuerdo nunca haberlo visto solucionado
Gracias por este tipo de trabajo. Ejercitar la mente siempre es bueno
No se si es el mismo caso que Ud. menciona, pero pero en el 75 o 76 (yo estaba en secundaria) se propagó un problema de este tipo, semejante a la segunda figura, de este artículo, pero con dos trazos más. Tambien se hablaba de un premio, según decían, de la embajada de la URSS. Ese, yo lo resolví, imagino que otros tambien, pero claro, con el "truquito" de un doblez en el papel. En la actual figura, tambien es fácil resolverlo con el truquito, que ya Nestor nos advierte que es "ilegal", así que no vale.
Corrección de memoria....en el caso antiguo, me parece que se permitía levantar el lápiz una vez
La verdad que me gustó mucho el reto y bueno también la explicación. Espero que no se demoren mucho en poner otros retos o problemas para darle solución, pues en el menor tiempo que tenga libre en mi casa o trabajo, poder ejercitar la mente sería muy bueno. Gracias
Por favor los fines de semana a muchos no es imposible acceder a esta pagina pues solo la vemos por el trabajo, a mi me encanta estos problemas...., hagan lo posible por ponerlos entre semana para todos podernos entretener y aprender
Por un punto donde convergen un número par de segmentos se entra y se sale, se entra y se sale, por lo que puede comenzarse fuera y se continúa fuera (no tiene ningún extremo de la línea) o puede comenzarse en él y terminar en él con lo que contendrá dos vértices, si todos los puntos tienen segmentos pares se comienza y termina en el mismo punto porque tendría los dos extremos de la línea.
En el caso de un punto con número impar de segmentos, o bien se comienza en él y se concluye fuera o se comienza fuera y se concluye en él por lo que tiene necesariamente un extremo de la linea.
Una línea sólo tiene dos extremos por lo que si hay un solo punto con segmentos impares o hay más de dos, no tiene solución porque en el primer caso buscamos una línea de un solo extremo y en el segundo caso con más de dos extremos.
Uff y yo rompiéndome la testa con la segunda figura. Fue bueno, ejercitamos la mente. Hasta hicimos competencia entre la familia y nada. Continuamos en la espera de otro problemita, gracias.
JAJAJA menos mal que leí el articulo antes de romperme mucho la cabeza, pero sí que trate de resolver la figura 2, pero ahora ya se la respuesta. Voy a darle duros a los intelectos de mi grupo social. Gracias
Por cierto de los 7 puentes originales solo quedan vivos tres, aunque sólo dos de ellos desde la época de Euler, pues uno fue reconstruido en 1935.
Es un juego. Parece cínico. Suena real. Pero es virtual. Imágenes de la percepción en torno a la acción. Irremediable no es una situación que describe lo hecho sino el desecho. Reciclar.
No era kaliningrado
Era Königsberg ciudad del imperio alemán, república de weimar y del tercer reich (soy consciente de que ese es la misma ciudad, pero estaría mal decir que se refería a la ciudad cuando estaba bajo el dominio de la URSS (Rusia todavía mantiene el control sobre la ciudad))
vaya... quería saber si podía recorrer una ciudad sin pasar 2 veces por la misma calle, pero veo que es imposible, gracias!
Cuales la respuesta
Tengo una figura,dos cuadros tengo que empezar de un punto.ciadrado lado derecho,cuadrado lado izquierdo sin levantar la mano