Un chícharo matemático y dos caramelitos
 Para no desencantar a quienes me retan a poner acertijos matemáticos de alto calibre, aquí va uno de estos. Y para no pecar de elitista, les planteo dos en que todos podrán ejercitar el intelecto, sin sufrir de siomates.
Para no desencantar a quienes me retan a poner acertijos matemáticos de alto calibre, aquí va uno de estos. Y para no pecar de elitista, les planteo dos en que todos podrán ejercitar el intelecto, sin sufrir de siomates.
I
Hallar, con demostración, el mayor número que sea el producto de números enteros positivos cuya suma sea igual a 1976. En mi respuesta se enterarán de un interesante testimonio, que acaba de cumplir 40 años.
Expresado en notación matemática sería así:
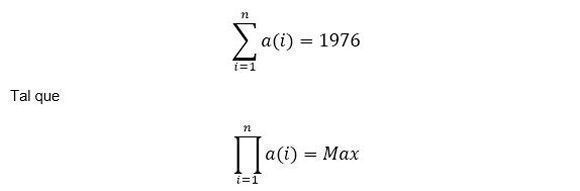
II
Si una tela de araña crece el doble de su tamaño cada día, y el día 20 cubre todo el agujero, qué día hubo de cubrir la mitad de dicho agujero
III
Y para ejercitar el pensamiento literario, les propongo dar una interpretación creativa a la siguiente oración del gran poeta cubano Eliseo Diego, que es utilizada muy frecuentemente en Radio Enciclopedia:
“Y no es por azar que nacemos en un sitio y no en otro, sino para dar testimonio”.
¡Manos y mente a la obra!
- Respuesta a “Psicología, matemática y Girón de la Victoria, a seis m”
- Psicología, matemática y Girón de la victoria, a seis m
- Respuesta a “Ecos de un encuentro inolvidable inspirado por la matemática y la creatividad”
- Ecos de un encuentro inolvidable inspirado por la matemática y la creatividad
- Respuesta a “La juventud, las probabilidades y un desmenuce de frase célebre”
- ir aPara Pensar... »
- Firman acuerdo de intercambio y cooperación partidos comunistas de Cuba y Chile
- Burkina Faso expulsa a tres diplomáticos franceses acusados de subversión
- Resultados Electrizantes en la Serie Nacional de Béisbol: Duelos Cerrados y Sorpresas en el Diamante
- Presidente de Adidas celebra vínculos con el deporte cubano
- Israel lanza ataques contra Irán, según funcionario estadounidense
- ir aNoticias »
- Respuesta a “Psicología, matemática y Girón de la Victoria, a seis m”
- Psicología, matemática y Girón de la victoria, a seis m
- S05E13: Un gladiador que regresa y el primer vistazo a la secuela de Joker
- Respuesta a “Ecos de un encuentro inolvidable inspirado por la matemática y la creatividad”
- Ecos de un encuentro inolvidable inspirado por la matemática y la creatividad
- ir aEntretenimiento »


hoy sí que no tengo las neuronas activadas, paso.
Esos acertijos estan muy faciles, por favor yo no respondo esas cosas de primaria!!!! lol
Cuando hablamos del producto de números enteros lo podemos simplificar finalmente al producto de dos números, es decir a*b, además del producto su suma también se resume en a+b y que debe ser igual al número propuesto 1976.
a+b=1976
a=(1976-b)
P_max=a*b
P_max=(1976-b)b
P_max=1976b-b^2
∂P/∂b=1976-2b=0
1976-2b=0
b=988
a=b
a=988
R/ El producto mayor es
P_max=976144
Camaradas, esto es lo mejor que pude hacer, un saludo
Cuando hablamos del producto de números enteros lo podemos simplificar finalmente al producto de dos números, es decir a*b, además del producto su suma también se resume en a+b y que debe ser igual al número propuesto 1976.
a+b=1976
a=(1976-b)
P_max=a*b
P_max=(1976-b)b
P_max=1976b-b^2
∂P/∂b=1976-2b=0
1976-2b=0
b=988
a=b
a=988
R/ El producto mayor es
P_max=976144
Camaradas, esto es lo mejor que pude hacer, un saludo
I. El mayor número es 2.6159878105133479515342408424316e+297 que es 2^988, ya que sumar 2 las 988 veces daría 1976.
En el caso de la tela de arana la mitad del agujero fue cubierto el dia 19. En el problema matematico solo de leerlo me dio dolor de cabeza, definitivamente la matematica no es lo mio. Suerte al que lo pueda resolver.
I- 988 * 988 = 976144 pues resultan de ser los 2 mayores numeros posittivos enteros q suman 1976. La demostración la debo pero en excel con el método de prueba y error llegué a este resultado q es el correcto.
II- Si cubre el 100% al día 20 y siempre cubría el doble del día anterior la mitad de lo q hizo el 20 lo tenía el día 19.
Saludos yumurinos.
I- x * n = 1976 -> x = 1976 / n
x ^ n = MAX -> (1976 / n) ^ n = MAX
se debe maximizar
f(n) = (1976 / n) ^ n
resulta x = 2 n = 988 MAX = 2.6159878105133479515342408424316e+297
II- La tela de araña cubre la mitad del agujero en 19 días
Saludos y gracias por este espacio de participación, que entretiene. 1era vez que me embullo.
Pedrada I
988 + 988 = 1976
988 * 988 = 976144 (Máx)
Para demostrar creo que hay que derivar y no recuerdo. Entonces, mejor por tanteo y lqqd, jeje.
Interpretación de solución II
Aparentemente la tela de araña cubriría la mitad del agujero el día 19; pero, según entiendo, por un tema gramatical del enunciado, crecer el doble cada día debería significar que, por ejemplo...
Si hoy yo mido 1,60m y crezco 5 cm al año, pues el próximo año mediré 1,65.
Si hoy yo mido 1,60m y crezco el doble de mi tamaño al año. Pues el año próximo mediré 1,60 + (1,60 * 2) = 4,80.
Asumiendo este ritmo de crecimiento y que sea uniforme por demás, pues la tela de araña cubriría la mitad del agujero, en algún momento entre el día 19 y antes de llegar al día 20. Al iniciar el día 19 la tela representaría un 33,33...%, para que al iniciar el día 20 logre el 100%.
Otra cosa sería si el enunciado dijera "duplica su tamaño cada día", cosa que personalmente interpreto muy diferente a "crecer el doble de su tamaño".
Mi poco creativa III.
La historia la contamos y en parte la hacemos los hombres, entendamos y aprovechemos el contexto que nos tocó vivir, es único. Cristobal Colón, de nacer en estos días, fuera posiblemente solo un famoso capitán de buque mercante o un gran pescador.
Me too L
ai
PROBLEMA I:
Solución: (3^658)x2 = 1,7652881309265063132182469752768e+314
Demostración:
Primeramente notemos que 1976=2x988. Luego la mayor cantidad de sumandos mayores que 1 en los que se puede descomponer 1976 es 988, con todos los sumando iguales a 2. El producto de estos sumandos es 2^988. Veamos ahora si existe un producto mayor:
Expresemos 1976 como 2+2+2+…+2 (con 988 sumandos) y veamos qué sucede con la productoria si introducimos un sumando mayor.
En el caso de que este sumando se pueda expresar de la forma 2k (par), podemos obtenerlo sustituyendo una cantidad k de sumandos 2 por su suma, el número 2k. Luego el nuevo producto será 2k(2^(988-k)). Demostremos que este producto es menor que el anterior.
2k(2^(988-k)) ≤ 2^988 2k ≤ 2^k k ≤ 2^(k-1)
Para probar esto procedamos por inducción.
Para k=1 y k=2 tenemos casos de igualdad. El caso k=3 cumple la desigualdad y será nuestra base de inducción. Entonces debemos probar que k+1 < 2^(k+1-1), es decir, k+1 1, entonces k+1 < 2k, pero 2k < 2^k por la hipótesis de la inducción, por lo que k+1 < 2^k y queda demostrado.
De esta forma la mayor productoria que se puede obtener con sumandos pares es 2^988.
Veamos ahora el caso de los impares. Notemos que como 1976 es par, siempre habrá una cantidad par de sumandos impares. Por tanto podemos agruparlos en parejas.
Introduzcamos entonces los sumandos a y b impares sustituyendo una cantidad (a+b)/2 de sumandos 2. De esta forma la nueva productoria será (2^(988-(a+b)/2))ab.
• Si a=b=1, la productoria es 2^987, que es menor que 2^988.
• Si a=1 y b=3, la productoria es 3(2^986), que también es menor que 2^988=4(2^986).
Demostremos por inducción que si a o b es 1, entonces el producto disminuirá en relación con 2^988. Nuestra base serán los casos anteriores. Digamos sin pérdida de generalidad que a=1. Luego:
(2^(988-(b+1)/2))b < 2^988 b < 2^((b+1)/2)
Digamos que existe un b que cumple esta condición. Como estamos tratando con casos impares, el próximo caso será b+2. Debemos probar entonces que b+2 < 2^((b+3)/2). Pero 2^((b+3)/2)=2^(((b+1)/2)+1)=2x2^((b+1)/2)=2^((b+1)/2)+2^((b+1)/2). Por la hipótesis de la inducción tenemos que b < 2^((b+1)/2) y además, como (b+1)/2 ≥ 1 porque b ≥ 1, entonces 2 ≤ 2^((b+1)/2). Sumando ambas relaciones obtenemos que
b+2 < 2^((b+1)/2)+2^((b+1)/2)=2^((b+3)/2)
Por tanto si a o b es 1, la productoria será menor. Veamos si a y b son mayores o iguales que 3.
• Si a=b=3, la productoria es 9(2^985), que sí es mayor que 2^988=8(2^985).
• Si a=3 y b=5 nuevamente la productoria es menor, 15(2^984) < 2^988=16(2^984)
• Si a=b=5 sucede lo mismo, 25(2^983) < 2^988=32(2^983).
Demostremos ahora por inducción que a partir de a=b=5, la productoria siempre será menor que 2^988. Nuestra base serán los dos últimos casos.
(2^(988-(a+b)/2))ab < 2^988 ab < 2^((a+b)/2)
Digamos que existen a y b que cumplen la condición. Probemos que se cumple también para a y b+2, es decir, que a(b+2) < 2^((a+b+2)/2).
Pero
a(b+2) < 2^((a+b+2)/2) ab+2a < 2^(((a+b)/2)+1) ab+2a < 2x2^((a+b)/2)
Pero como b ≥ 3, entonces 2a < ab y por tanto ab + 2a < 2ab. Y como 2ab < 2x2^((a+b)/2) por la hipótesis de la inducción, entonces queda probado que de esta manera siempre se obtendrá una productoria menor que 2^988.
Por tanto la única manera de superar este número es sustituyendo grupos de 3 sumandos 2, por parejas de sumandos 3. Al hacer la mayor cantidad posible de estas sustituciones obtenemos que la mayor productoria es (3^658)x2
Buscamos un numero que sumado x veces resulte 1796:
n * x = 1976
despejamos x:
x = 1976 / n
La multiplicación de los números que sumados dan 1976 debe ser la máxima posible:
n ^ x = MAX -> n ^(1976 / n) = MAX
debemos hallar un entero n lo más cercano posible a un máximo de f(n)
f(n) = n ^ (1976 / n)
Para hallar los máximos buscamos dos ceros de la derivada de f(n)
f'(n) = 0
el único cero de esta derivada es
n = e = 2.718281828459045
probamos los resultadon con los enteros más cercanos a e (euler) que son 2 y 3
-para 2
sumatoria: 2 * 988 = 1976
productoria: 2 ^ 988 = 2.6159878105133479515342408424316e+297
-para 3
sumatoria: 3 * 658 + 2 = 1976
productoria: 3 ^ 658 * 2 = 1.7652881309265063132182469752768e+314
por tanto: la sumatoria que maximiza la productoria es 3 * 658 + 2 = 1976
Solución: (3^658)x2 = 1,7652881309265063132182469752768e+314
Demostración:
Primeramente notemos que 1976=2x988. Luego la mayor cantidad de sumandos mayores que 1 en los que se puede descomponer 1976 es 988, con todos los sumando iguales a 2. El producto de estos sumandos es 2^988. Veamos ahora si existe un producto mayor:
Expresemos 1976 como 2+2+2+…+2 (con 988 sumandos) y veamos qué sucede con la productoria si introducimos un sumando mayor.
En el caso de que este sumando se pueda expresar de la forma 2k (par), podemos obtenerlo sustituyendo una cantidad k de sumandos 2 por su suma, el número 2k. Luego el nuevo producto será 2k(2^(988-k)). Demostremos que este producto es menor que el anterior.
2k(2^(988-k)) ≤ 2^988 2k ≤ 2^k k ≤ 2^(k-1)
Para probar esto procedamos por inducción.
Para k=1 y k=2 tenemos casos de igualdad. El caso k=3 cumple la desigualdad y será nuestra base de inducción. Entonces debemos probar que k+1 < 2^(k+1-1), es decir, k+1 1, entonces k+1 < 2k, pero 2k < 2^k por la hipótesis de la inducción, por lo que k+1 < 2^k y queda demostrado.
De esta forma la mayor productoria que se puede obtener con sumandos pares es 2^988.
Veamos ahora el caso de los impares. Notemos que como 1976 es par, siempre habrá una cantidad par de sumandos impares. Por tanto podemos agruparlos en parejas.
Introduzcamos entonces los sumandos a y b impares sustituyendo una cantidad (a+b)/2 de sumandos 2. De esta forma la nueva productoria será (2^(988-(a+b)/2))ab.
• Si a=b=1, la productoria es 2^987, que es menor que 2^988.
• Si a=1 y b=3, la productoria es 3(2^986), que también es menor que 2^988=4(2^986).
Demostremos por inducción que si a o b es 1, entonces el producto disminuirá en relación con 2^988. Nuestra base serán los casos anteriores. Digamos sin pérdida de generalidad que a=1. Luego:
(2^(988-(b+1)/2))b < 2^988 b < 2^((b+1)/2)
Digamos que existe un b que cumple esta condición. Como estamos tratando con casos impares, el próximo caso será b+2. Debemos probar entonces que b+2 < 2^((b+3)/2). Pero 2^((b+3)/2)=2^(((b+1)/2)+1)=2x2^((b+1)/2)=2^((b+1)/2)+2^((b+1)/2). Por la hipótesis de la inducción tenemos que b < 2^((b+1)/2) y además, como (b+1)/2 ≥ 1 porque b ≥ 1, entonces 2 ≤ 2^((b+1)/2). Sumando ambas relaciones obtenemos que
b+2 < 2^((b+1)/2)+2^((b+1)/2)=2^((b+3)/2)
Por tanto si a o b es 1, la productoria será menor. Veamos si a y b son mayores o iguales que 3.
• Si a=b=3, la productoria es 9(2^985), que sí es mayor que 2^988=8(2^985).
• Si a=3 y b=5 nuevamente la productoria es menor, 15(2^984) < 2^988=16(2^984)
• Si a=b=5 sucede lo mismo, 25(2^983) < 2^988=32(2^983).
Demostremos ahora por inducción que a partir de a=b=5, la productoria siempre será menor que 2^988. Nuestra base serán los dos últimos casos.
(2^(988-(a+b)/2))ab < 2^988 ab < 2^((a+b)/2)
Digamos que existen a y b que cumplen la condición. Probemos que se cumple también para a y b+2, es decir, que a(b+2) < 2^((a+b+2)/2).
Pero
a(b+2) < 2^((a+b+2)/2) ab+2a < 2^(((a+b)/2)+1) ab+2a < 2x2^((a+b)/2)
Y como b ≥ 3, entonces 2a < ab y por tanto ab + 2a < 2ab. Y como 2ab < 2x2^((a+b)/2) por la hipótesis de la inducción, entonces queda probado que de esta manera siempre se obtendrá una productoria menor que 2^988.
Por tanto la única manera de superar este número es sustituyendo grupos de 3 sumandos 2, por parejas de sumandos 3. Al hacer la mayor cantidad posible de estas sustituciones obtenemos que la mayor productoria es
(3^658)x2
lqqd
Para resolver el primer problema podemos remitirnos a los fundamentos de la derivación para encontrar máximos y mínimos. Como nos están preguntando por el mayor número que sea el producto de números enteros positivos y que su suma sea igual a 1976 podríamos comenzar planteando que:
1- Producto(max)=aXb
Como quiera que a+b=1976:
2- b=1976-a
sustituimos en 1:
3- Producto(max)=aX(1976-a)
Producto(max)=1976a-a2 (a al cuadrado, mi teclado no tiene signo de elevado al cuad.)
Derivando Producto(max) en función de a tenemos:
4- Producto(max)=1976-2a
Igualando a cero tenemos:
5- 1976-2a=0
a=1976/2
a=988
sustituyendo en 2:
6- b=1976-988
b=988
respondiendo la pregunta 988 es el mayor número cuya suma sea igual a 1976 y el producto de ellos sea máximo.
Aplicaciones prácticas de este procedimiento se pueden encontrar en el calculo de los costos máximos y minimos de productos, dimensiones máximas de envoltorios y cajas, en agronomía para la planificación eficiente de areas de cultivos etc.
El segundo problema es mas difícil porque acabamos de resolver un problema donde aplicamos formulas y calculo diferencial y nuestro cerebro como que se queda ¨conectado¨ y no nos deja ver que este no se resuelve con el mismo procedimiento matematico. Para los que terminaron mas lucidos el primer problema y se dieron cuenta que si la tela de araña crece el doble por día y el día 20 cubre el agujero completo entonces el 19 cubriría la mitad, nada de cálculos complejos, puro razonamiento, observación y concentración.
A veces queremos mirar tan, pero tan lejos, que ni siquiera percibimos los que esta delante de nuestros ojos.
Saludos
Pioneer y Pavel dieron excelente respuesta a la I, por supuesto no hay otra. La II es muy fácil, el día 19, o sea el anterior al doblaje siguiente cuando ya se cubre el agujero. Entonces voy a la Interpretación creativa para la oración: “Y no es por azar que nacemos en un sitio y no en otro, sino para dar testimonio”.
Ellos, los que nacieron y vieron salir al Sol para luego quedar sembrados como raíces, esos nos hablan a través de sus huesos. Nos alzan los brazos para saludarnos desde la tierra que los cubrió un día. Están hablándonos al pie de los cimientos de los muros ancestrales que fueron testigos de batallas inmemoriles, con sus trazos desde las cuevas que sirvieron de refugio a hombres y animales. Desde los panteones violados, antes vedados por siglos, nos hablan de lo que hubo y lo que queda. Por los hombres que nacieron y murieron en el lugar, conocemos el camino transitado. Ellos estuvieron allí para certificarlo, y nosotros estamos hoy para contarlo, para seguir hablando al que escucha y quiere saber. Nacemos y morimos para estar juntos: las piedras y los huesos. Para dar evidencia de vida antes de perdernos en el tiempo, en tanto luego nazcan otros más como aquellos o como nosotros, que vengan a preguntarnos.
Para resolover este ejercicio, planteamos el problema de otra manera.
Veamos que la segunda ecuacion mostrada, Prod( a(i) ) = Max es igual a (1976/i)^i. Por tanto este problema es equivalente a encontrar el valor maximo de la función (1976/i)^i, donde 'i' es la cantidad de sumandos y también es la cantidad de divisores enteros.
Para encontrar este valor máximo, derivamos la función respecto a 'i' e igualamos a cero, depejamos la 'i' y obtenemos que el valor de 'i' donde esta función alcanza un máximo es: 1976/e (donde e es igual al número de Euler).
Dado que hemos hecho el tratamiento en los reales esta 'i' hallada no tiene por que ser un divisor entero de 1976, de hecho, no lo es, por tanto la solución es encontrar el divisor entero 'k' de 1976 más cercano al 'i' encontrado, o sea k = minarg(módulo(x-'i')) y 1976 = k*q con q entero y distinto de 1.
Para resolver esto hallamos el q de la ecuación 1976 = 'i'*q. En este caso q=e (con e = al número de Euler). Como 1976 no es divisible por el entero más cercano a 'e' que es 3, entonces los valores posibles de q serían, 2 o 4. Sean k1= 1976/2 y k2=1976/4, se cumple que módulo(k1-'i')>módulo(k2-'i'), por tanto el valor buscado es k2.
Luego la soluciòn se obtiene sustituyendo ´i´ por k2 en la función inicial (1976/i)^i. como k2 es 1976/4= 494, entonces el máximo es (1976/494)^494 = 4^494.
Por inducción se puede demostrar que el producto máximo se logra descomponiendo el número en factores de 3. Si el número es de la forma 3*n (multiplo de 3) el producto mayor es 3^n. Si es de la forma 3*n+2 el producto mayor es 2*(3)^n. Y si es de la forma 3*n+1 el producto mayor es 4*(3)^(n-1). Como 1976= 3*658+2 entonces el producto máximo es 2*(3)^658.
Mande un.comentario con mi respuesta hace Como 6 horas y no lo han publicado , aqui va mi respuesta , pido disculpas so esta doble
La pregunta dice la Suma de NUMEROSSS, no la Suma de Dos numeros por tanto si tenemos que 1976= 988*2 o lo que es lo mismo 2+2+2+2+2+2....988 veces entonces El producto de estos numeros enteros positivos (la pregunta no dice que no puedan ser iguales ) es 2*2*2*2*2.....988 veces o lo que es lo mismo 2 elevado a la 988 , so alguien tiene tiempo que calcule El numero, pero a mi no SE me ocurre UN numero mayor que ese que cumpla Las condiciones planteadas
Saludos
3*658+2 = 1976
a(i){i=1..658} = 3, a(659) = 2
n = 659
MAX = 2 * 3^658
Demostracion:
Todos los numeros enteros se pueden descomponer en sumandos de 1. Pero el producto de numeros 1 es igual a 1, no nos sirve.
Todos los numeros enteros se pueden descomponer en sumandos de 2, y un 3 si es impar.
Pero para maximizar el producto, el menor numero que se puede descomponer tanto en sumandos de 2 como de 3 es 6,
y: 6 = 2 + 2 + 2, o 6 = 3 + 3. Pero 2*2*2 = 8 < 3*3=9
Luego es mejor descomponer en sumandos de 3.
Todos los numeros enteros se pueden descomponer en sumandos de 3, y uno o dos 2.
Si es multiplo de 3: en m 3
Si deja resto 1 en la division por 3: en m-2 3 + 2 + 2
Si deja resto 2 en la division por 3: en m-1 3 + 2
Y:
5 < 3*2
7 3. Sea este a(n) sin perdida de generalizacion.
Sea M = producto de los a(1)..a(n-1)
Luego, supuesto Max = M*a(n)
Como a(n)>3, sea B tal que a(n)=3+B
Luego:
M*a(n) > M*3*B (por ser M*a(n) supuesto Max, y a(i),3,B la alternativa descomponiendo a(n))
a(n) > 3*B
3+B > 3*B
3 > 2*B
Solucion cuando B 8.
Por lo que seria mejor descomponer 2+4 en 3+3.
En caso que fuese un par mayor que 2, repetimos el procedimiento anterior para obtener otro sumando 4, donde:
4 + 4 = 8, 4*4 = 16, pero 8=3+3+2 donde 3*3*2 = 18 >16.
Luego, la descomposicion optima es 658 3 y un 2.
Al parecer la conversion a HTML eliminó varios pedazos entre los "menor_que" y los "mayor_que" al interpretarlos como etiquetas.
La segunda parte debe decir:
Si es multiplo de 3: en m 3
Si deja resto 1 en la division por 3: en m-2 3 + 2 + 2
Si deja resto 2 en la division por 3: en m-1 3 + 2
Y:
5 < 3*2
7 3. Sea este a(n) sin perdida de generalizacion.
Sea M = producto de los a(1)..a(n-1)
Luego, supuesto Max = M*a(n)
Como a(n)>3, sea B tal que a(n)=3+B
Luego:
M*a(n) > M*3*B (por ser M*a(n) supuesto Max, y a(i),3,B la alternativa descomponiendo a(n))
a(n) > 3*B
3+B > 3*B
3 > 2*B
Solucion para B=1, por lo que a(n)=4.
Pero para 1976, 1976-4 = 1972 que no es multiplo de 3, por lo que tiene que aparecer otro sumando par. (ya vimos que 1 no sirve)
Si fuese 2, nos quedarian los sumandos 2 y 4 donde 2*4=8, pero 2+4=6 que es tambien 3+3 y 3*3=9 > 8.
Por lo que seria mejor descomponer 2+4 en 3+3.
En caso que fuese un par mayor que 2, repetimos el procedimiento anterior para obtener otro sumando 4, donde:
4 + 4 = 8, 4*4 = 16, pero 8=3+3+2 donde 3*3*2 = 18 >16.
Luego, la descomposicion optima es 658 3 y un 2.
Para ampliar mi respuesta del comentario anterior donde expuse que El resultado era 2^988 , mi solucion tambien aplica para 2*3^658 y para 4^494 puesto que:
2^988=2*3^658=4^494.... SE pueden encontrar infinitas soluciones para este resultado que es el mayor que yo encontre.
A quienes me escriben, tengan paciencia que pronto comenzarán a publicarse sus respuestas. Les alerto que habrá lindas sorpresas
La respuesta a la 2da es muy sencilla, además de haber sido respondida ya correctamente en varias ocasiones. La 3era, bueno, me gustan los números y no las letras. En cuanto a la 1era, muchos usuarios han dado como respuesta final 976 144. No lo considero correcto ya que para llegar a ese resultado acotan sus cálculos a sólo 2 productos (a*b=988*988=988^2=976 144). En el enunciado del problema nuncan nos restringen en este aspecto, por lo cual el mayor producto sería 2.61*10^297, correspondiente con el resultado de 2^988, siendo 988*2=1976.
La respuesta a la 2da es muy sencilla, además de haber sido respondida ya correctamente en varias ocasiones. La 3era, bueno, me gustan los números y no las letras. En cuanto a la 1era, muchos usuarios han dado como respuesta final 976 144. No lo considero correcto ya que para llegar a ese resultado acotan sus cálculos a sólo 2 productos (a*b=988*988=988^2=976 144). En el enunciado del problema nuncan nos restringen en este aspecto, por lo cual el mayor producto sería 2.61*10^297, correspondiente con el resultado de 2^988, siendo 988*2=1976. La demostración no la describo porque me quedó un poco extensa. En caso de estar bien, debe haber una solución más eficiente.
La respuesta a la 2da es muy sencilla, además de haber sido respondida ya correctamente en varias ocasiones. La 3era, bueno, me gustan los números y no las letras. En cuanto a la 1era, muchos usuarios han dado como respuesta final 976 144. No lo considero correcto ya que para llegar a ese resultado acotan sus cálculos a sólo 2 productos (a*b=b*b=988*988=988^2=976 144). En el enunciado del problema nuncan nos restringen en este aspecto, por lo cual el mayor producto sería 2.61*10^297, correspondiente con el resultado de 2^988, siendo 988*2=1976. La demostración no la describo porque me quedó un poco extensa. En caso de estar bien, debe haber una solución más eficiente.
Publiquenme!!!
La respuesta a la 2da es muy sencilla, además de haber sido respondida ya correctamente en varias ocasiones. La 3era, bueno, me gustan los números y no las letras. En cuanto a la 1era, muchos usuarios han dado como respuesta final 976 144. No lo considero correcto ya que para llegar a ese resultado acotan sus cálculos a sólo 2 productos (a*b=b*b=988*988=988^2=976 144). En el enunciado del problema nuncan nos restringen en este aspecto, por lo cual el mayor producto sería 2.61*10^297, correspondiente con el resultado de 2^988, siendo 988*2=1976. La demostración no la describo porque me quedó un poco extensa. En caso de estar bien, debe haber una solución más eficiente.
Y el II:
el dia 19. Un caramelito!!!!!!
En el III hay que escribir mucho, incluso más de lo que escribí en el primero, jajaja
Que paso con mi respuesta que no la publicaron.
A mi me da PI.
Los que contestaron que el número es 2 mas 3 por 658 y que por lo tanto el producto es 2 por 3 elevado a la potencia 658 dieron la respuesta correcta.
La demostración está dada por:
1.Todo número mayor que 4 se puede representar por una suymatoria cuyo producto es mayor que el propio número.
2, El número 1 no debe pertenecer a la sumatoria pues no influye en el producto.
3. El menor número cuyo producto con otro numero es mayor que en una sumatoria es el número 3.
4. Todo número mayor que 4 puede ser representado por 3x mas 2p donde p puede ser o, 1 o 2.
En nuestro caso el número es 3 por 658 mas 2.
Hoy 15 de julio muere en EEUU la destacada matemática Iraní Maryam Mirzakhani convaleciente de un cáncer de mama con infiltración de medula ósea, su Frase “La belleza de las matemáticas solo se le muestra a los seguidores más pacientes” es un himno para los matemáticos modernos , es la única mujer que obtuvo la medalla Fields , obtuvo su doctorado en Harvard en el 2004, su campo de estudio se encontraba entre la geometría algebraica y la diferencial , se destacó también en la física teórica en el campo de la multidimensionalidad, amó tanto las formas geométricas que su sueño de ser novelista quedo atrapada en la geometría, sirva de honor este pequeño recordatorio entre tantos matemáticos del debate para llegar a esta eminente mujer que nos quiso hacer soñar con los números y el cáncer solo la dejó hacer el esbozo de su obra.